Intro
This page describes many of the different aspects of number theory our students explored during the past summers. We don’t expect you to have even heard of the mathematical objects on this page, but this is our chance to tell you about them and convince you that they are cool.
Sums of two squares
According to Carl Friedrich Gauss, “Mathematics is the queen of sciences and number theory is the queen of mathematics.” Number theory is the study of solutions to equations where the variables must take on values that are whole numbers or ratios of whole numbers.
In a letter written on December 25, 1640, Pierre de Fermat stated the following theorem.
Theorem (Fermat): If \(n\) is a positive integer, then there are integers \(x\) and \(y\) so that \(x^{2} + y^{2} = n\) if and only if in the prime factorization of \(n\), $$n = \prod_{i=1}^{k} p_{i}^{r_{i}}$$ all primes \(p_{i} \equiv 3 \pmod{4}\) are raised to even powers.
For example, \(5040 = 2^{4} \cdot 3^{2} \cdot 5 \cdot 7\) cannot be written as a sum of two squares because \(7\) occurs to an odd power, while \(2210 = 2 \cdot 5 \cdot 13 \cdot 17\) can be. In fact,
\begin{align*}
2210 &= 1^{2} + 47^{2}\\
&= 19^{2} + 43^{2}\\
&= 23^{2} + 41^{2}\\
&= 29^{2} + 37^{2}.
\end{align*}(Pierre de Fermat stated that he had a solid proof of this fact, but he did not share his proof of it with anyone. Leonhard Euler was the first to publish a proof.) We will use Fermat’s theorem as motivation to introduce to you things about quadratic forms, algebraic number theory, elliptic curves and modular forms.
Now that you know Fermat’s theorem, you can take your favorite sequence of integers and ask which terms are sums of two squares. The following two results were proven by Keenan Curtis (a Wake Forest undergraduate who graduated in the spring of 2014).
Theorem: We have that \(2^{n} + 1\) is a sum of two squares if and only if \(n\) is even or \(n = 3\).
Theorem: Suppose that \(n\) is odd and \(3^{n} + 1\) is a sum of two squares. Then \(n\) is a sum of two squares.
For example, $$3^{65} + 1 = 1580199068031288^{2} + 2793568035017330^{2}$$ is a sum of two squares, and therefore \(65 = 8^{2} + 1 = 7^{2} + 4^{2}\) must be a sum of two squares also.
Proving Fermat’s theorem
The first crucial observation needed to prove Fermat’s theorem is that if \(n = a^{2} + b^{2}\) and \(m = c^{2}+d^{2}\) are both sums of two squares, then $$mn = (ac+bd)^{2} + (ad-bc)^{2}$$ is also a sum of two squares. The main remaining step is to determine which primes numbers can be a sum of two squares. A necessary condition for a prime \(p\) to be a sum of two squares is for there to be some integer \(a\) with \(a^{2} \equiv -1 \pmod{p}\). Fermat’s Little Theorem states that if \(p\) is prime and \(\gcd(a,p) = 1\), then \(a^{p-1} \equiv 1 \pmod{p}\). Applying Fermat’s little theorem, we see that if there is an \(a\) with \(a^{2}\equiv -1\pmod{p}\) then \(1 \equiv a^{p-1} \equiv (-1)^{\frac{p-1}{2}} \pmod{p}\), which implies that \(p=2 \text{ or } p \equiv 1 \pmod{4}\). It takes more work to prove that if \(p \equiv 1 \pmod{4}\) is prime (like \(p = 27109\), Wake Forest University’s zip code), then \(p\) is a sum of two squares. The first observation necessary is that there is a solution to \(a^{2} \equiv -1 \pmod{p}\). In fact, Wilson’s theorem shows that \(\left(\frac{p-1}{2}\right)!^{2} + 1 \equiv 0 \pmod{p}\). The final step is very clever and involves the following lemma.
Lemma: Let \(p\) be a prime and let \(a\) be a natural number not divisible by \(p\). Then there exist integers \(x\) and \(y\) such that \(ax \equiv y \pmod{p}\) with \(0 < |x|, |y| < \sqrt{p}\). (This is Lemma 8.15 from Number Theory Through Inquiry, the red book pictured on the home page.)
Applying the lemma with \(a\) satisfying \(a^{2} \equiv -1 \pmod{p}\) gives integers \(x\) and \(y\) so that \(0 < x^{2} + y^{2} < 2p\) and \(x^{2}+y^{2}\equiv 0 \pmod{p}\). This means that \(x^{2}+y^{2}\) must equal \(p\), so \(p\) is a sum of two squares!
The geometry of numbers
The previous lemma really comes from the geometry of numbers. This corner of number theory plays a role in the study of quadratic forms and in algebraic number theory. A lattice \(L\) in \(\mathbb{R}^{n}\) is a collection of vectors in \(\mathbb{R}^{n}\) so that (i) if \(\vec{x}, \vec{y} \in L\), then \(\vec{x}+\vec{y} \in L\), (ii) if \(\vec{x} \in L\) then \(-\vec{x} \in L\), (iii) the elements in \(L\) span \(\mathbb{R}^{n}\). The first key result from the geometry of numbers is Minkowski’s theorem. To state it, we define the covolume \(d(L)\) of a lattice \(L\) to be the volume of the “fundamental parallelepiped” spanned by a generating set for \(L\). Minkowski’s theorem states the following.
Minkowski’s Theorem: Let \(S \subseteq \mathbb{R}^{n}\) be a bounded, convex set with the property that if \(\vec{x} \in S\), then \(-\vec{x} \in S\). If the volume of \(X\) is greater than \(2^{n} d(L)\), then \(S\) contains a nonzero point in \(L\).
The lemma above can be proven by fixing an \(a \in \mathbb{Z}\) with \(a^{2} \equiv -1 \pmod{p}\) and defining \(L = \{ (x,y) \in \mathbb{Z}^{2} : x \equiv ay \pmod{p} \}\). This turns out to be a lattice with covolume \(p\). Pick a real number \(s\) greater than \(\sqrt{p}\) but less than \(\lceil \sqrt{p} \rceil\). Now, let \(S\) be the square with vertices \( (\pm s, \pm s) \). The area of \(S\) is greater than \(4p\) and so Minkowski’s theorem applied to \(S\) guarantees the existence of a point \((x,y) \in L\) with \( 0 < |x|, |y| < \sqrt{p} \) and \( x \equiv ay \pmod{p} \). (This argument is closely related to that in Theorem 7.2 of Algebraic Number Theory and Fermat’s Last Theorem, also pictured on the home page.)
Algebraic number theory
Let \(i\) be a square root of \(-1\). The set \(\mathbb{Z}[i] = \{ a + bi : a, b \in \mathbb{Z} \}\) is called the collection of Gaussian integers. The elements in this set are all algebraic integers — they are roots of polynomials with integer coefficients and leading coefficient \(1\). This set has the structure of a ring, since one can add and multiply Gaussian integers. It turns out that just like the ring of ordinary integers, every element of the Gaussian integers can be factored into products of powers of Gaussian primes. This factorization is unique (up to the order of the factors, and multiplication by units: \(1, i, -1, \text{ and } -i\)). For example, \(2 = (-i) (1+i)^{2}\). Here \(-i\) is a unit, and \(1+i\) is a Gaussian prime. The number \(3\), on the other hand, remains prime in \(\mathbb{Z}[i]\). The function \(N : \mathbb{Z}[i] \to \mathbb{Z}\) given by \(N(a+bi) = a^{2}+b^{2}\) is called the norm map, and it is multiplicative (\(N(\pi_{1} \pi_{2}) = N(\pi_{1}) N(\pi_{2})\)). These facts can be used to prove that every prime \(p \equiv 1 \pmod{4}\) can be written as a sum of two squares. The reason is that \(p\) divides \(\left(\frac{p-1}{2}\right)!^{2} + 1 = \left(\left(\frac{p-1}{2}\right)! + i\right) \left(\left(\frac{p-1}{2}\right)! – i \right)\), but it does not divide either of the two factors on the right hand side, and so \(p\) cannot be a Gaussian prime. Thus, \(p = \pi_{1} \pi_{2}\) admits a non-trivial factorization (with \(1 < N(\pi_{1}), N(\pi_{2}) < N(p) = p^{2}\)). This implies that \(N(\pi_{1}) = N(\pi_{2}) = p\). If \(\pi_{1} = a+bi\), then \(p = a^{2}+b^{2}\).
The key in this instance is that \(\mathbb{Z}[i]\) had the unique factorization property. This, however, is not always true. A number field \(K\) is a collection of algebraic numbers that is closed under addition, subtraction, multiplication and division (of nonzero elements), and that also is finite-dimensional (when thought of as a vector space over \(\mathbb{Q}\)). If \(K\) is a number field, the set \(\mathcal{O}_{K}\) of algebraic integers in \(K\) is also a ring with many desirable properties, but it need not have the unique factorization property. For example, if \(d > 0\) is a squarefree integer and \(K = \{ a + b \sqrt{-d} : a, b \in \mathbb{Q} \}\), then \(K\) is a field. The ring \(\mathcal{O}_{K}\) is then equal to either \(\{ a + b \sqrt{-d} : a, b \in \mathbb{Z} \}\) or \(\{ a + b \frac{1 + \sqrt{-d}}{2} : a, b \in \mathbb{Z} \}\), depending on whether \(d \equiv 1 \text{ or } 2 \pmod{4}\) or \(d \equiv 3 \pmod{4}\). It is a deep theorem of Baker, Heegner and Stark that \(\mathcal{O}_{K}\) has the unique factorization property if and only if \(d = 1, 2, 3, 7, 11, 19, 43, 67 \text{ or } 163\). The proof of this theorem relies on properties of elliptic curves and modular forms.
Elliptic curves
An elliptic curve is a curve with an equation of the form \( y^2 = x^{3} + ax + b \). Elliptic curves are not ellipses. Rather, the theory of elliptic curves evolved from the problem of determining an exact formula for the arc length of an ellipse. Elliptic curves have unusual richness and structure, much of which stems from the following observation. If \(P\) and \(Q\) are two different points on \(E\), then the line through \(P\) and \(Q\) intersects the curve \(E\) at exactly one other point \(R\).
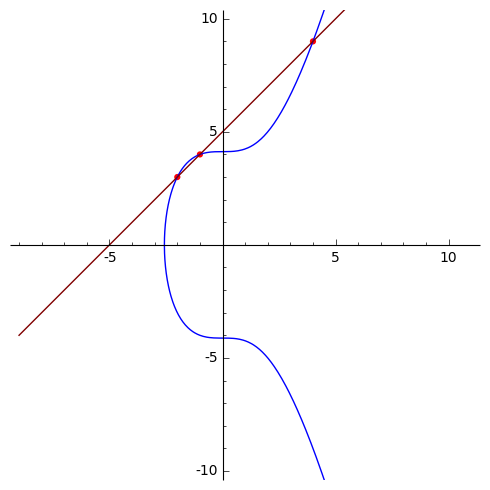
The elliptic curve \(y^2 = x^3 + 17\). The line through the points \( P=(-2,3) \) and \(Q= (-1,4) \) intersects the curve at \( R=(4,9) \).
If \(P=(a,b)\) and \(Q=(c,d)\) have coordinates that are both rational numbers, then the slope and \(y\)-intercept of this line will be rational as well. This makes it so \(R=(x,y)\) has rational coordinates as well. We define \(P+Q=(x,-y)\), which is the result of reflecting \(R\) across the line of symmetry \(y=0\).
This “addition” operation gives the set of rational points \(E(\mathbb{Q})\) the structure of an abelian group. It is easy to see that \(P+Q=Q+P\). However, the associative law \((P+Q)+R = P+(Q+R)\) is fairly difficult to prove. (In order for everything to be well-defined, we actually need to work in projective space with the equation \(y^{2} z = x^{3} + axz^{2} + bz^{3}\). This equation is homogeneous, and adds an extra point where \(x = 0, y = 1, z = 0\). This added point, the “point at infinity” is the identity of the abelian group.) If \(P\) is a point in \(E(\mathbb{Q})\), we write \(mP\) for the point obtained by adding \(P\) to itself \(m\) times.
Theorem (Mordell, 1920): If \(E\) is an elliptic curve, all the points in \(E(\mathbb{Q})\) can be generated from a finite collection.
In spite of Mordell’s theorem, there is still no algorithm that is proven to compute the finite collection of generators for \(E(\mathbb{Q})\), or even to compute the number of generators (known as the rank of \(E\)). In the case of \(E : y^{2} = x^{3} + 17\), every point in \(E(\mathbb{Q})\) can be written uniquely as \(mP+nQ\) where \(P = (-2,3), Q=(-1,4)\). (A fancier way of saying this is that the abelian group \( E(\mathbb{Q}) \cong \mathbb{Z} \times \mathbb{Z} \).)
If \(E : y^{2} = x^{3} + ax + b \) with \( a, b \in \mathbb{Z} \), then we can look at points on the elliptic curve mod \(p\), and we denote this finite set by \( E(\mathbb{F}_{p}) \). It turns out that the number of points in this set is always close to \(p+1\).
Theorem (Hasse, 1936): If \(p\) is a prime, the number of points in \( E(\mathbb{F}_{p})\) is \( p + 1 – a_{p}(E) \), and \( |a_{p}(E)| \leq 2 \sqrt{p} \).
Using these numbers \(a_{p}(E)\), we can define the \(L\)-function \(L(E,s)\) by the infinite product $$L(E,s) = \prod_{p \text{ prime}} \left(1 – a_{p}(E) p^{-s} + p^{1-2s}\right)^{-1} = \sum_{n=1}^{\infty} \frac{a_{n}(E)}{n^{s}}.$$ This series converges if \( s > 3/2 \), but the modularity of elliptic curves (eventually completed in 1999 by Breuil, Conrad, Diamond, Taylor, Wiles, etc.) gives an alternative definition of the function \( L(E,s) \) which is valid for all \(s\) (even complex values of \(s\)). We can now state the following.
Conjecture (Birch and Swinnerton-Dyer, 1965): The function \( L(E,s) \) has a zero at \(s = 1\) of order equal to the rank of \(E\).
Note that this conjecture predates the knowledge that \(L(E,s)\) is defined at \(s = 1\). This conjecture is one of the Millennium Problems. Its resolution carries a 1 million dollar prize.
Applications of elliptic curves
The numbers \(48\), \(49\) and \(50\) are consecutive. The first is three times a square, the second is a square, and the third is twice a square. Does this ever happen again? That is, is there an integer solution to the system of equations \begin{align*} y^{2} – 3x^{2} &= 1 \\ 2z^{2} – y^{2} &= 1 \end{align*} with \(3x^{2} > 48\)? It turns out the answer is no. The reason is that this system of equations can be put in the form of an elliptic curve \( E : y^{2} = x^{3} – 36x \). This elliptic curve has infinitely many rational points on it (generated by \( (0,0), (6,0), \text{ and } (18,72) \)), but a theorem of Siegel proves that there are only finitely many points \( (x,y) \) where \(x\) and \(y\) are both integers. The largest integral point on \(E\) is \( (294,5040) \), and this corresponds to the solution \(48,49,50\) solution.
What do elliptic curves have to do with Fermat’s theorem that if \(p \equiv 1 \pmod{4} \) is prime, then \(p = a^{2} + b^{2}\) for some integers \(x\) and \(y\)? If \(E : y^{2} = x^{3} – x\) and \(p \equiv 1 \pmod{4} \), then if we define the number \(a\) by \(a_{p}(E) = 2a\), there is an integer \(b\) so that \(p = a^{2} + b^{2}\). Since there are fast algorithms for counting points on elliptic curves, this gives a quick way to find, given a prime \(p \equiv 1 \pmod{4}\) integers \(a\) and \(b\) so that \(p = a^{2} + b^{2}\). (However, this is not the fastest such method. The multiplicative group mod \(p\) is cyclic, which means that if we pick some number \(r\) at random, there is a 50% chance that \(x \equiv r^{\frac{p-1}{4}} \pmod{p}\) is a square root of \(-1 \pmod{p}\). Once we have found an \(x\) so that \(x^{2} \equiv -1 \pmod{p}\), we use the Euclidean algorithm in \(\mathbb{Z}[i]\) to compute \( a+bi=\gcd(x+i,p) \). Then \(a^{2}+b^{2}=p\).)
Modular forms
According to Barry Mazur,
Modular forms are function on the complex plane that are inordinately symmetric. They satisfy so many internal symmetries that their mere existence seem like accidents. But they do exist.
Let \( \mathbb{H} = \{ x + iy : x \in \mathbb{R}, y > 0 \} \). Roughly speaking, a modular form of weight \(k\) and level \(N\) is a differentiable function \( f : \mathbb{H} \to \mathbb{C} \) that satisfies transformation laws of the form $$ f\left(\frac{az+b}{cz+d}\right) = (cz+d)^{k} f(z) $$ for all \(2 \times 2\) matrices \(\left[ \begin{matrix} a & b \\ c & d \end{matrix} \right]\) with determinant \(1\) for which \(c\) is a multiple of \(N\). Any modular form has a power series expansion involving \(q = e^{2 \pi i z}\) of the form $$f(z) = \sum_{n=0}^{\infty} a(n) q^{n}.$$ Modular forms can be built using the Dedekind \(\eta\)-function, which is defined in terms of the infinite product \(\eta(z) = q^{1/24} \prod_{n=1}^{\infty} (1-q^{n})\).
The coefficients of modular forms have a number of interesting properties. Let \(p(n)\) be the number of partitions of \(n\), that is, the number of ways to write \(n\) as the sum of a sorted sequence of positive integers. For example, \(p(4)=5\), because there are \(5\) partitions of \(4\), namely \(4 = 3+1 = 2+2 = 2+1+1 = 1+1+1+1.\) Euler found the identity $$ \sum_{n=0}^{\infty} p(n) q^{n} = \prod_{n=1}^{\infty} \frac{1}{1-q^{n}},$$ and the right hand side is also equal to \(q^{1/24}/\eta(z)\). Ramanujan used ideas from the theory of modular forms to show that \(p(5n+4) \equiv 0 \pmod{5}\) for all positive integers \(n\). Also, Ramanujan conjectured that the coefficients of \begin{align*} \Delta(z) &= q \prod_{n=1}^{\infty} (1-q^{n})^{24}\\ &= \sum_{n=1}^{\infty} \tau(n) q^{n}\\ &= q – 24q^{2} + 252q^{3} – 1472q^{4} + \cdots \end{align*} (a modular form of weight \(12\) and level \(1\)) satisfy \begin{align*} \tau(mn) &= \tau(m) \tau(n) \text{ if } \gcd(m,n) = 1\\ \tau(p^{k}) &= \tau(p) \tau(p^{k-1}) – p^{11} \tau(p^{k-2}) \text{ if } p \text{ is prime. } \end{align*} (These conjectures were proven by Mordell.) Another interesting result is the following.
Theorem (Lagrange, 1770): Every positive integer can be written as a sum of four integral squares.
Using modular forms this is straightforward to prove. Moreover, one can get a formula for the number of representations. For a positive integer \(n\), let \(\sigma(n)\) denote the sum of the divisors of \(n\). Then the number of ways that \(n\) can be written in the form \(x^{2}+y^{2}+z^{2}+w^{2}\) with \(x,y,z,w \in \mathbb{Z}\) is \( 8 \sigma(n) – 32 \sigma(n/4)\) (if \(n\) isn’t a multiple of 4, we define \(\sigma(n/4) = 0\)).
The 1999 proof of the modularity of elliptic curves forges an intimate link between these two types of objects. In particular, if \(E\) is an elliptic curve with rational coefficients, there is a modular form \(f_{E}(z)\) of weight \(2\) for which $$f_{E}(z) =\sum_{n=1}^{\infty} a_{E}(n) q^{n},$$ where the numbers \(a_{E}(n)\) are the same as those in the definition of \(L(E,s)\). For example, if \(E : y^{2} = x^{3} – x \), the corresponding modular form is $$ \eta(4z)^{2} \eta(8z)^{2} = q \prod_{n=1}^{\infty} (1-q^{4n})^{2} (1-q^{8n})^{2},$$ and has level \(32\). As a consequence if \(p\) is prime, the \(p\)th coefficient of this power series tells you how you can write \(p\) as a sum of two squares! The connection between elliptic curves and modular forms also gives a method that sometimes allows one to find a generator for the group of rational points \(E(\mathbb{Q})\).
We conclude with several interrelated facts that are manifestations of the very deep and very beautiful theory of complex multiplication. (i) The number $$e^{\pi \sqrt{163}} \approx 262537412640768743.99999999999925$$ is very, very close to a whole number. (ii) The polynomial \(x^{2} + x + 41\) takes prime values for \(0 \leq x \leq 39\) (note that the discriminant of this polynomial is \( 1^{2} – 4 \cdot 1 \cdot 41 = -163\)). (iii) The ring \( \{ a + b \frac{1 + \sqrt{-163}}{2} : a, b \in \mathbb{Z} \}\) has the unique factorization property.